Question

Slender rod is 90.0 cm long and has mass 0.120 kg. A small 0.0200 kg sphere is welded to one end of the rod, and a small 0.0400 kg sphere is welded to the other end. The rod, pivoting about a stationary, frictionless axis at its center, is held horizontal and released from rest.

Answer 1

The linear speed is 1.33 m/s.

Step-by-step explanation:

Given that,

Length of rod = 90.0 cm

Mass of slender rod = 0.120 kg

Mass of small sphere = 0.0200 kg

Mass of another small sphere = 0.0400 kg

Suppose, we need to find the linear speed of the 0.0500-kg sphere as it passes through its lowest point?

We need to calculate the the change in potential of the complete system

Using formula of change in potential

m₂ and m₃ are the masses at the rod ends.

The rod center of mass neither gains nor loses potential

`\Delta U=m_(2)gy_(2)+m_(3)gy_(3)`

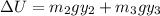
Put the value into the formula

`\Delta U=0.0400*9.8*(-45*10^(-2))+0.0200*9.8*45*10^(-2)`

`\Delta U=-0.0882\ N-m`

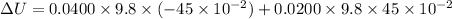
We need to calculate the moment of inertia of the rod

Using formula of moment of inertia of the rod

`I_(1)=2\rho \int_(0)^(r)(r^2 dr)`

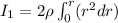
Put the value into the formula

`I_(1)=2*(0.120)/(90*10^(-2)) \int_(0)^(0.45)(r^2 dr)`

`I_(1)=2*(0.120)/(90*10^(-2))*(((0.45)^3)/(3)-0)`

`I_(1)=0.0081\ kg-m^2`

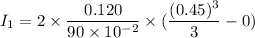
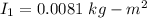
We need to calculate the moment of inertia of the end masses

Using formula of moment of inertia

`I_(2+3)=\sum mr^2`

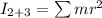
Put the value into the formula

`I_(2+3)=(0.0400+0.0200)*0.45^2`

`I_(2+3)=0.01215\ kg-m^2`

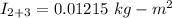
We need to calculate the change in potential energy to the system kinetic energy

Using formula of kinetic energy

`\Delta U=K.E`

`\Delta U=(1)/(2)(I_(1)+I_(2+3))\omega^2`

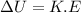
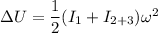
Put the value into the formula

`0.0882=(1)/(2)(0.0081+0.01215)\omega^2`

`\omega^2=(2*0.0882)/(0.02025)`

`\omega=\sqrt{(2*0.0882)/(0.02025)}`

`\omega=2.95\ rad/s`

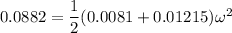
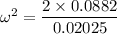
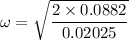
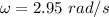
We need to calculate the linear speed

Using formula of linear speed

`v = r\omega`

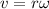
Put the value into the formula

`v=0.45*2.95`

`v=1.33\ m/s`

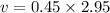
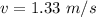
Hence, The linear speed is 1.33 m/s.