Question

Express the rate of reaction in terms of the change in concentration of each of the reactants and products: A(g) + 2B(g) → C(g) Rate = − Δ[A] Δt = − 2 1 Δ[B] Δt = Δ[C] Δt Rate = − Δ[A] Δt = − Δ[B] Δt = Δ[C] Δt Rate = − Δ[A] Δt = − 1 2 Δ[B] Δt = Δ[C] Δt When [B] is decreasing at 0.28 mol/L·s, how fast is [A] decreasing?

Answer 1

The correct expression for rate of reaction is:

`Rate=-(d[A])/(dt)=-(1)/(2)(d[B])/(dt)=+(d[C])/(dt)`

The [A] decreasing at 0.14 mol/L.s

Explanation :

The given rate of reaction is,

`A(g)+2B(g)\rightarrow C(g)`

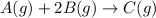
The expression for rate of reaction :

`\text{Rate of disappearance of A}=-(d[A])/(dt)`

`\text{Rate of disappearance of B}=-(1)/(2)(d[B])/(dt)`

`\text{Rate of formation of C}=+(d[C])/(dt)`

So,

`Rate=-(d[A])/(dt)=-(1)/(2)(d[B])/(dt)=+(d[C])/(dt)`

Now we have to calculate how fast is [A] decreasing.

Given:

`-(d[B])/(dt)=0.28mol/L.s`

`-(1)/(2)(d[B])/(dt)=-(1)/(2)* 0.28mol/L.s=-0.14mol/L.s`

`-(d[A])/(dt)=-(1)/(2)(d[B])/(dt)=-0.14mol/L.s`

Hence, the [A] decreasing at 0.14 mol/L.s