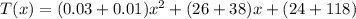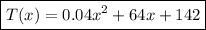Question

Please help

generator 1: C(x) = 0.03x^2+26x+24
generator 2: K(x) = 0.01x^2+38x+118

write a function rule for the sum of the costs of these two generators. Enter your answers in the boxes.

T(x) = C(x) + K(x)

T(x) = (0.03+ ? )x^2 + (26+38)x +(24+118)
T(x) = ?x^2 + ?x + ?

SOLVE FOR THE BLANKS. PREFERABLY WITH STEPS SHOWN.
Thank you ​

Answer 1

`T(x)= 0.04x^2+64x+142`

Explanation:

Sum of Functions

We are given the functions for the cost of two generators:

`C(x) = 0.03x^2+26x+24`

`K(x) = 0.01x^2+38x+118`

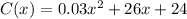
We are required to find the function for the sum of the costs of the two generators:

T(x)= C(x)+K(x)

We'll add both functions:

`T(x)= 0.03x^2+26x+24+ 0.01x^2+38x+118`

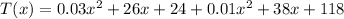
To find the sum of both functions, we collect like terms:

`T(x)= (0.03+0.01)x^2+(26+38)x+(24+118)`

`\boxed{T(x)= 0.04x^2+64x+142}`