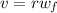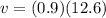Question

To throw a discus, the thrower holds it with a fully out-stretched arm. Starting from rest, he begins to turn with a con-stant angular acceleration, releasing the discus after making one complete revolution. The diameter of the circle in which the discus moves is about 1.8 m. If the thrower takes 1.0 s to complete one revolution, starting from rest, what will be the speed of the discus at release?

Answer 1

11.3m/s

Step-by-step explanation:

We can find the solution through the rotational motion of the discus,

`\theta = w_it+(1)/(2)\alpha t^2`

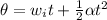
Where,

`\theta = 2\pi`

`w_i=0`

`t=1s`

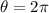
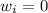
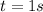
Solving to find
`\alpha`,

`2\pi = (0)(1)+(1)/(2)\alpha (1)^2`

`\alpha = (2\pi)/(0.5)`

`\alpha = 12.6 rad/s^2`

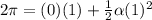
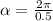
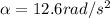
Therefore we can find the final angular velocity, through the rotational motion equation given by,

`w_f = w_i + \alpha t`

Substituting,

`w_f = 0 + 12.6*(1)`

`w_f =12.6rad/s`

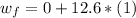
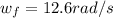
The diameter of the circle is 1.8m, then the ratio will be the half, i.e,

`r=0.9m`

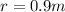
The relation between linear velocity and angular velocity is

`v=rw_f`

`v=(0.9)(12.6)`

`v=11.3m/s`