Question

Assume that the Poisson distribution applies and that the mean number of hurricanes in a certain area is 5.4 per year. a. Find the probability​ that, in a​ year, there will be 3 hurricanes. b. In a 45​-year ​period, how many years are expected to have 3 ​hurricanes? c. How does the result from part​ (b) compare to a recent period of 45 years in which 5 years had 3 ​hurricanes? Does the Poisson distribution work well​ here?

Answer 1

a) There is a probability of 12% that 3 hurricanes happens in any year.

b) It is expected that 5.4 years in a period of 45 years have 3 hurricanes.

c) The Poisson distribution work well in predicting this kind of events.

Explanation:

The Poisson distribution has the following expression

`P(x=k)=(\lambda^ke^(-\lambda))/(k!)`

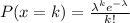
In this case we have
`\lambda=5.4`. The probability that, in a year, there will be 3 hurricanes is:

`P(x=3)=(5.4^3e^(-5.4))/(3!)=(0.71)/(6)=0.12`

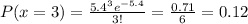
There is a probability of 12% that 3 hurricanes happens in any year.

If we take a period of 45 years, the expected amount of years with 3 hurricanes can be estimated as:

`Y=45*0.12=5.4`

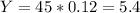
It is expected that 5.4 years in a period of 45 years have 3 hurricanes.

The Poisson distribution work well in predicting this kind of events.