Question

In a lab experiment, two identical gliders on an air track are held together by a piece of string, compressing a spring between the gliders. While they are moving to the right at a common speed of 0.500 m/s, one student holds a match under the string and burns it, letting the spring force the gliders apart. One glider is then observed to be moving to the right at 1.300 m/s. (the string and spring both have negligible mass).(a) What velocity does the other glider have? (b) Is the total kinetic energy of the two gliders after the collision greater than, less than, or equal to the total kinetic energy before the collision? If greater, where did the extra energy come from? If less, where did the "lost" energy go?

Answer 1

Part a)

`v_2 = -0.300`

Part b)

Here final kinetic energy is more than the initial kinetic energy

This increase in kinetic energy is due to spring connected between them as the spring energy is converted into kinetic energy of two blocks

Step-by-step explanation:

Part a)

As we know that there is no external force on the system of two gliders

So here we can use momentum conservation for two gliders

So we will have

`m_1 v_1 + m_2 v_2 = (m_1 + m_2)v_i`

`m_1 = m_2`

`1.300 + v_2 = 2(0.500)`

`v_2 = -0.300`

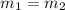
Part b)

now we will have

initial kinetic energy of both gliders is given as

`K_i = (1)/(2)(m + m)(0.500)^2`

`K_i = 0.25m`

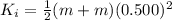
Final kinetic energy of two gliders

`K_f = (1)/(2)m(0.300)^2 + (1)/(2)m(1.300)^2`

`K_f = 0.89 m`

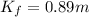
so here final kinetic energy is more than the initial kinetic energy

This increase in kinetic energy is due to spring connected between them as the spring energy is converted into kinetic energy of two blocks