Question

Three forces act on an object. Two of the forces are at an angle of to each other and have magnitudes N and N. The third is perpendicular to the plane of these two forces and has magnitude N. Calculate the magnitude of the force that would exactly counterbalance these three forces.

Answer 1

Step-by-step explanation:

Assuming that all forces extend from the origin point, with
`F_1` and
`F_2` lying in the xy plane, so
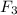`F_3` is along the z axis. So, we have:

`\vec{F_1}=F_1\hat{i}+0\hat{j}+0\hat{k}\\\vec{F_2}=F_2cos\theta\hat{i}+F_2sin\theta\hat{j}+0\hat{k}\\\vec{F_3}=0\hat{i}+0\hat{j}+F_3\hat{k}`

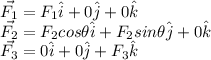
The net force is:

`\vec{F}=\vec{F_1}+\vec{F_2}+\vec{F_3}\\\vec{F}=(F_1+F_2cos\theta)\hat{i}+F_2sin\theta\hat{j}+F_3\hat{k}`

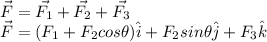
The force (
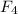`F_4`) that would exactly counterbalance these three forces will be opposite in direction and equal in magnitude to the net force:

`\vec{F_4}=-(F_1+F_2cos\theta)\hat{i}-F_2sin\theta\hat{j}-F_3\hat{k}\\F_4=√((-(F_1+F_2cos\theta))^2+(-F_2sin\theta)^2+(-F_3)^2)`