Question

Given the function, f(x)= √ x+2-3 choose the correct transformation

1) left 2, down 3
2) left 2, up 3
3) right 2, down 3
4) right 2, up 3

Answer 1

1) left 2, down 3

Explanation:

Given:

The function is,
`f(x)=√(x+2)-3`

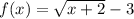
Here, the parent function is square root function.

So, Let
`g(x)` be the parent function.

∴
`g(x)=√(x)`

Now, in order to transform
`g(x)` to
`f(x)`, first, we need to add 2 to x and is given by the rule:

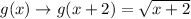`g(x)\rightarrow g(x+2)=√(x+2)`. From the transformation rules, if a positive number is added to x, then the graph shifts left.

Hence, the graph of
`g(x)` will shift left by 2 units.

Now, next we need to add -3 to
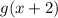`g(x+2)` to get the given function
`f(x)`. The rule is given as:

`g(x+2)\rightarrow g(x+2) - 3=√(x+2)-3=f(x)`.

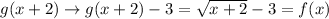As per transformation rules, if a negative number is added to the function, the graph shifts down.

Here, the graph of
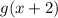`g(x+2)` will shift down by 3 units.

Overall, the parent function
`g(x)=√(x)` can be transformed to
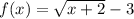`f(x)=√(x+2)-3` by shifting the parent function graph 2 units left and 3 units down.

So, option 1 is correct.