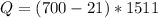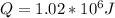A) We know that efficiency in a system is defined by the equation
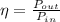
Where P is the Power in a system. Then,
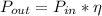
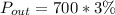

Therefore the output power is 21W
B) Work is defined by,
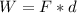
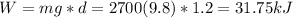
To calculate the power we know that is the rate of work in a determined time, then
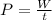
Re-arrange for t,
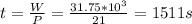
c) Finally we have that the amount of heat wasted depends on the power, then,