Question

Prior to the discovery that freon-12 (CF 2 Cl 2 ) was harmful to the Earth’s ozone layer, it was frequently used as the dispersing agent in spray cans for hair spray, etc. Its enthalpy of vaporization at its normal boiling point of − 29.2°C is 20.25 kJ mol − 1 . Estimate the pressure that a can of hair spray using freon-12 had to withstand at 40°C, the temperature of a can that has been standing in sunlight. Assume that ∆ vap H is a constant over the temperature range involved and equal to its value at − 29.2°C.

Answer 1

9.10 atm

Step-by-step explanation:

At the normal boiling point, the vapor pressure of a liquid is equal to the atmospheric pressure, 1 atm. Because ΔHvap doesn't change, we can use the Clausius-Clayperon equation to determinate the pressure at the other temperature.

So, for p1 = 1 atm, T1 = -29.2ºC + 273 = 243.8 K, T2 = 40ºC + 273 = 313 K, R = 8.3145 J/molK (gas constant):

`ln((p2)/(p1) ) = (DHvap)/(R) ((1)/(T1) - (1)/(T2))`

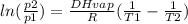
ln(p2/1) = (20250/8.3145)*(1/243.8 - 1/313)

ln(p2) = 2435.50424*9.068x10⁻⁴

ln(p2) = 2.2086

p2 =
`e^(2.2086)`

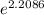
p2 = 9.10 atm