Question

Given: f(x) = 1/x+5 and g(x) = x - 2.

What are the restrictiorts of the domain of f(g(x))?
0 x4 -5
O X-3
OX= 2
There are no restrictions.

Answer 1

The restriction of the domain of f(g(x)) is that x cannot be 3.

Explanation:

The first step to solve this question is finding the function, replacing the values. So

`f(x) = (1)/(x+5)`

`g(x) = x - 2`

`f(g(x)) = f(x - 2) = (1)/(x - 2 + 5) = (1)/(x - 3)`

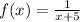
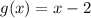
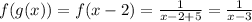
The function is a fraction, which means that the restriction is that the denominator cannot be zero. So

`x - 3 \\eq 0`

`x \\eq 3`

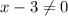
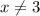
The restriction of the domain of f(g(x)) is that x cannot be 3.