Question

Steam flows steadily through an adiabatic turbine. The inlet conditions of the steam are 4 MPa, 500°C, and 80 m/s, and the exit conditions are 30 kPa, 92 percent quality, and 50 m/s. The mass flow rate of the steam is 12 kg/s. Determine (a) the change in kinetic energy, (b) the power output, and (c) the turbine inlet area.

Answer 1

a)23.4KW

b)12.11MW

c)1.155m^2

Step-by-step explanation:

Hello!

To solve this problem follow the steps below

1. We will call 1 at the turbine entrance and 2 at the exit.

2. To calculate the change in kinetic energy, calculate the kinetic energy at the entrance and exit of the turbine and find the difference.

E=0.5mV^2

m=mass flow=12kg/s

E=kinetic energy

V=speed

solving

`E=(0.5)(12kg/s)(80m/S)^2-(0.5)(12kg/s)(50m/S)^2=23400W=23.4KW`

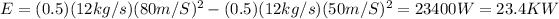
3. We find the enthalpies in states 1 and 2, and the density in the state 2 by thermodynamic tables

note: Through laboratory tests, thermodynamic tables were developed, these allow to know all the thermodynamic properties of a substance (entropy, enthalpy, pressure, specific volume, internal energy etc ..)

through prior knowledge of two other properties such as pressure and temperature.

h1=Enthalpy(Water;T=500C;P=4000kPa)

=3445KJ/kg

h2=Enthalpy(Water;x=0,92(quality);P=30kPa)=2438KJ/kg

density2=0.2078kg/m^3

4.

use the first law of thermodynamics that states that the energy entering the system is the same as the one that must go out, consider the flow energy, the work done and the kinetic energy

`mh1+0.5mV1^2=mh2+W+0.5mV2^2\\W=m(h1-h2)+0.5m(V1^2-V2^2)\\W=12(3445000-2438000)+0.5(12)(80^2-50^2)=12107400W=12.11MW`

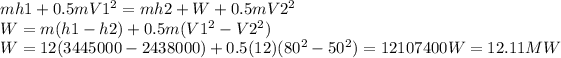
5.

to find the speed at the exit of the turbine we remember that the mass flow is defined as the product between the velocity density and the cross-sectional area

m=(density)(A2)V2

`A2=(m)/((density)(V2)) =(12)/((0.2078)(50))=1.155m^2`