Answer:
2.1844 m/s
Step-by-step explanation:
The principle of conservation of momentum can be applied here.
when two objects interact, the total momentum remains the same provided no external forces are acting.
Consider the whole system , gun and bullet. as an isolated system, so the net momentum is constant. In particular before firing the gun, the net momentum is zero. The conservation of momentum,
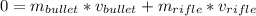
assume the bullet goes to right side and the gravitational acceleration =10
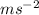
so now the weight of the rifle=
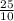
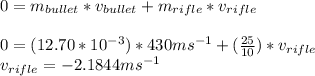
this is a negative velocity to the right side. that means the rifle recoils to the left side