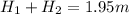Question

The initial speed of each block is v0 = 6.92 m/s, and each incline slopes upward at an angle of θ = 50.0°. The block on the shorter track leaves the track at a height of H1 = 1.25 m above the ground. Find (a) the height H for the block on the longer track and (b) the total height H1 + H2 for the block on the shorter track.

Answer 1

Part a)

`H = 2.44 m`

Part b)

`H_1 + H_2 = 1.95 m`

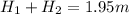
Step-by-step explanation:

Part a)

As we know that there is no friction on the inclined plane

So we can use energy conservation for both planes

For longer plane we will have

`mgH = (1)/(2)mv^2`

`H = (v^2)/(2g)`

`H = (6.92^2)/(2(9.81))`

`H = 2.44 m`

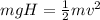
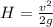
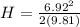
Part b)

On shorter plane the speed while it leave the plane at height H1 is given as

`(1)/(2)m(v_f^2 - v_i^2) = -mgH_1`

`(1)/(2)m(v_f^2 - 6.92^2) = -(9.81)(1.25)`

`v_f = 4.83 m/s`

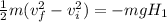
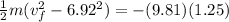
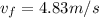
now the maximum height of projectile is given as

`H_2 = (v_f^2 sin^2\theta)/(2g)`

`H_2 = (4.83^2sin^2(50))/(2(9.81))`

`H_2 = 0.70 m`

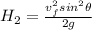
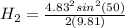
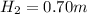
so we have

`H_1 + H_2 = 1.25 + 0.7`

`H_1 + H_2 = 1.95 m`