Answer:
How many units need to be sold to produce the maximum revenue? 1000 units
How many in dollars is the maximum revenue when the maximum of units are sold? $350,000
Explanation:
We get max value of a function if we differentiate it and set it equal to 0.
We need to differentiate r(x) and set it equal to 0 and solve for x.
That would be number of units sold to get max revenue.
Then we take that "x" value and substitute into r(x) to get the max revenue amount.
Before differentiating, we see the rules shown below:

Where
f'(x) is the differentiated function
Now, let's do the process:
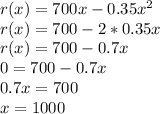
So, 1000 units need to be sold for max revenue
Now, substituting, we get:
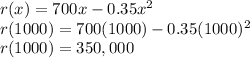
The max revenue amount is $350,000