Answer:

Step-by-step explanation:
Let's use the equation that relate the temperatures and volumes of an adiabatic process in a ideal gas.
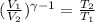 .
.
Now, let's use the ideal gas equation to the initial and the final state:

Let's recall that the term nR is a constant. That is why we can match these equations.
We can find a relation between the volumes of the initial and the final state.

Combining this equation with the first equation we have:
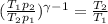
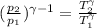
Now, we just need to solve this equation for T₂.

Let's assume the initial temperature and pressure as 25 °C = 298 K and 1 atm = 1.01 * 10⁵ Pa, in a normal conditions.
Here,

Finally, T2 will be:
