Answer:
27.35m
Step-by-step explanation:
For the calculation of the Support Force we rely on the formula for obtaining the force in a cylinder of a certain length l,
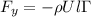
Here each term is,
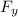 = Lift force
= Lift force
 = density of air
= density of air
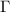 = vortex strength
= vortex strength
For this last equation, its mathematical representation is given by,
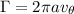
Here each term is,
a= 1m, radios of cylinder
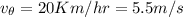 , the velocity of cylinder surface.
, the velocity of cylinder surface.
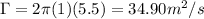
In order to find the density of the area at 2000m we will refer to the table of Standard Atmosphere of the United States, that is

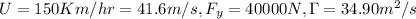
Replacing the values,
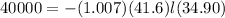
Clearing l and solving for it we have,
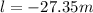
In this way we can conclude that the length of the cylinder must be 27.35m