Answer:
(x,y) = (-5,8)
Explanation:
The given equations are:
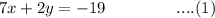
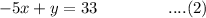
Equation (2) can be written as:
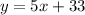
The value of
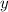 is now substituted in Equation (1).
is now substituted in Equation (1).
∴ Equation (1) becomes
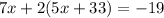
⇒
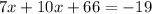
⇒ 17x = - 85
⇒ x = -5
Now substitute the value of x in (2) to get the value of y.
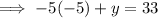
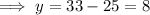
∴ y = 8
The ordered pair is (x,y) = (-5,8)