Question

A searchlight is 210 ft from a straight wall. As the beam moves along the​ wall, the angle between the beam and the perpendicular to the wall is increasing at the rate of 2.0 degrees divided by s. How fast is the length of the beam increasing when it is 290 ft​ long?

Answer 1

The length of the beam increasing is 9.64 ft/s.

Step-by-step explanation:

Given that,

Height = 210 ft

Distance =290 ft

According to figure,

We need to calculate the angle

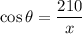`\cos\theta=(210)/(x)`....(I)

Put the value of x in the equation

`\cos\theta=(210)/(290)`

`\cos\theta=(21)/(29)=0.72`

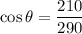
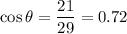
Now,
`\sin\theta=(20)/(29)`

On differentiate of equation (I)

`-\sin\theta(d\theta)/(dt)=-(-210)/(x^2)(dx)/(dt)`

`\sin\theta=(210)/(x^2)(dx)/(dt)`

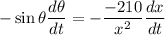
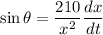
Put the value in the equation

`\sin(20)/(29)*2.0=(210)/((290)^2)(dx)/(dt)`

`(dx)/(dt)=\sin(20)/(29)*2.0*(290^2)/(210)`

`(dx)/(dt)=9.64\ ft/s`

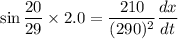
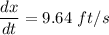
Hence, The length of the beam increasing is 9.64 ft/s.