Question

A completely inelastic collision occurs between two balls of wet putty that move directly toward each other along a vertical axis. Just before the collision, one ball, of mass 3.0 kg, is moving upward at 20 m/s and the other ball, of mass 2.0 kg, is moving downward at 12 m/s. How high do the combined two balls of putty rise above the collision point?

Answer 1

h = 2.64 meters

Step-by-step explanation:

It is given that,

Mass of one ball,
`m_1=3\ kg`

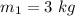
Speed of the first ball,
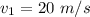`v_1=20\ m/s` (upward)

Mass of the other ball,
`m_2=2\ kg`

Speed of the other ball,
`v_2=-12\ m/s` (downward)

We know that in an inelastic collision, after the collision, both objects move with one common speed. Let it is given by V. Using the conservation of momentum to find it as :

`V=(m_1v_1+m_2v_2)/(m_1+m_2)`

`V=(3* 20+2* (-12))/(3+2)`

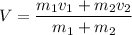
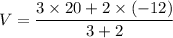
V = 7.2 m/s

Let h is the height reached by the combined balls of putty rise above the collision point. Using the conservation of energy as :

`mgh=(1)/(2)mV^2`

`h=(V^2)/(2g)`

`h=(7.2^2)/(2* 9.8)`

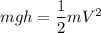
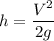
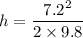
h = 2.64 meters

So, the height reached by the combined mass is 2.64 meters. Hence, this is the required solution.