Question

What are the coordinates of the circumcenter of this triangle?

Enter your answer in the boxes.

(
,
)

A right triangle A B C is shown on a coordinate plane. A is located at begin ordered pair negative 3 comma 5 end ordered pair. B is located at begin ordered pair negative 2 comma negative 1 end ordered pair. C is located at begin ordered pair 8 comma negative 1 end ordered pair

Answer 1

(3,2)

Explanation:

I took the test!

Answer 2

The coordinates of the circumcenter of this triangle are (3,2)

Explanation:

we know that

The circumcenter is the point where the perpendicular bisectors of a triangle intersect

we have the coordinates

`A(-2,5),B(-2,-1),C(8,-1)`

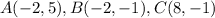
step 1

Find the midpoint AB

The formula to calculate the midpoint between two points is equal to

`M=((x1+x2)/(2),(y1+y2)/(2))`

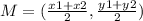
substitute the values

`M=((-2-2)/(2),(5-1)/(2))`

`M_A_B=(-2,2)`

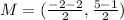
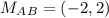
step 2

Find the equation of the line perpendicular to the segment AB that passes through the point (-2,2)

Is a horizontal line (parallel to the x-axis)

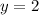`y=2` -----> equation A

step 3

Find the midpoint BC

The formula to calculate the midpoint between two points is equal to

`M=((x1+x2)/(2),(y1+y2)/(2))`

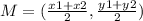
substitute the values

`M=((-2+8)/(2),(-1-1)/(2))`

`M_B_C=(3,-1)`

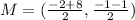
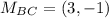
step 4

Find the equation of the line perpendicular to the segment BC that passes through the point (3,-1)

Is a vertical line (parallel to the y-axis)

`x=3` -----> equation B

step 5

Find the circumcenter

The circumcenter is the intersection point between the equation A and equation B

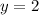`y=2` -----> equation A

`x=3` -----> equation B

The intersection point is (3,2)

therefore

The coordinates of the circumcenter of this triangle are (3,2)