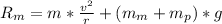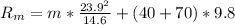Answer:
a) v=23.9 m/s
b) R=2646 N
Step-by-step explanation:
According to Newton's second law the net force at the top is given by
∑F=-m*ac
according to
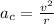
∑F=

a).
To lose contact this means that R=0 so the final equation is
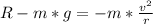

Solve to v
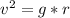
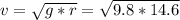
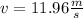
b).
v is the twice of part a so


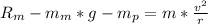
Solve to Rm