Question

A bank loaned out $37,500, part of it at the rate of 11% annual interest, and the rest at 9% annual interest. The total interest earned for both loans was $3,745.00. How much was loaned at each rate?

Answer 1

The Loan amount at 11 % interest rate is $ 18,500 And

The Loan amount at 9 % interest rate is $ 19,000

Explanation:

Given as :

Let The loan given at interest rate of 11 % annual = $ x

And The loan given at interest rate of 9 % annual = ($37,500 - $ x)

Total interest fro both loan = $3745

I.e CI 1 + CI 2 = $3745

Now, From compound interest method :

`Amount= Principal* (1 + (Rate)/(100))^(Time)`

`A 1 = $ 1* (1 + (11)/(100))^(1)`

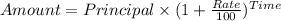
Or, A 1 = $ 1.11 x

Similarly

`A 2 = ($37,500 -x ) * (1 + (9)/(100))^(1)`

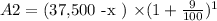
Or, A 2 = 1.09 × ($37,500 - $ x)

∵ Compound Interest = Amount - principal

Or, $ 3745 = CI 1 + CI 2

Or, $ 3745 = ($ 1.11 x - $ x) + ( 1.09 × ($37,500 - $ x) - ($37,500 - $ x) )

Or, $ 3745 = $ .11 x+ ($37,500 - $ x) ( .09 )

Or, $ 3745 = $ .02 x + $ 3375

or, 0.02 x = $ 3745 - $ 3375

∴ x = $
`(370)/(.02)`

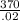
SO, x = $ 18,500

And $ 37500 - x = $ 19,000

Hence The Loan amount at 11 % interest rate is $ 18,500 And

The Loan amount at 9 % interest rate is $ 19,000 Answer