For this case we must resolve the following inequality:
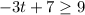
Subtracting 7 from both sides of the inequality we have:
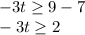
Dividing by 3 to both sides of the inequality we have:
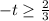
We multiply by -1 on both sides, taking into account that the sense of inequality changes:
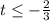
Thus, it is observed that to solve the inequality it is necessary to change the meaning of it.
ANswer:
False. It is necessary to change the sense of inequality