Question

Find x so that x, X +2, X'+3 are the first three terms of a geometric sequence. Then find the 5" term of the

sequence.

Answer 1

The fifth term is -1/4.

Explanation:

We know that the first three terms of the geometric sequence is x, x + 2, and x + 3.

So, our first term is x.

Then our second term will be our first term multiplied by the common ratio r. So:

`x+2=xr`

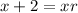
And our third term will be our first term multiplied by the common ratio r twice. Therefore:

`x+3=xr^2`

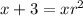
Solve for x. From the second term, we can divide both sides by x:

`\displaystyle r=(x+2)/(x)`

Substitute this into the third equation:

`\displaystyle x+3=x\Big((x+2)/(x)\Big)^2`

Square:

`\displaystyle x+3 = x\Big( ((x+2)^2)/(x^2) \Big)`

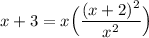
Simplify:

`\displaystyle x+3=((x+2)^2)/(x)`

We can multiply both sides by x:

`x(x+3)=(x+2)^2`

Expand:

`x^2+3x=x^2+4x+4`

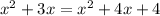
Isolate the x:

`-x=4`

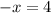
Hence, our first term is:

`x=-4`

Then our common ratio r is:

`\displaystyle r=((-4)+2)/(-4)=(-2)/(-4)=(1)/(2)`

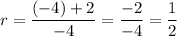
So, our first term is -4 and our common ratio is 1/2.

Then our sequence will be -4, -2, -1, -1/2, -1/4.

You can verify that the first three terms indeed follow the pattern of x, x + 2, and x + 3.

So, our fifth term is -1/4.