Question

A viscous fluid is flowing through two horizontal pipes. The pressure difference P1 - P2 between the ends of each pipe is the same. The pipes have the same radius, although one is twice as long as the other. How does the volume flow rate QB in the longer pipe compare with that in the shorter pipe?

Answer 1

Answer:half of shorter Pipe

Step-by-step explanation:

Fluid is Flowing through two horizontal pipes with pressure difference

`P_1-P_2=\Delta P`

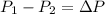
Both pipes have same radius

Length of one Pipe is twice of other

Let Longer Pipe be denote by 1 and smaller by 2

From Hagen Poiseuille equation

`\Delta P=(128\mu L\cdot Q)/(\pi D^4)`

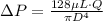
Where
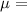`\mu =`viscosity of medium

L=length of Pipe

Q=discharge

D=diameter

For longer Pipe

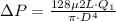`\Delta P=(128\mu 2L\cdot Q_1)/(\pi \cdot D^4)`----1

For smaller Pipe

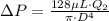`\Delta P=(128\mu L\cdot Q_2)/(\pi \cdot D^4)`------2

From 1 & 2 we get

`2L\cdot Q_1=L\cdot Q_2`

`Q_2=2Q_1`

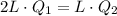
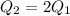
volume flow rate of longer pipe is half of smaller pipe