The acorn falls for approximately 0.902 seconds before landing on the dog's head.
How to get the time of fall
![\[ \text{Distance fallen} = (1)/(2) * \text{acceleration due to gravity} * \text{time}^2 \]](https://img.qammunity.org/2020/formulas/physics/middle-school/bwfpfwlv47z2275l68zoojnobl3ysmi9jw.png)
Given that the acorn falls 4.0 meters and assuming the acceleration due to gravity g is approximately
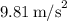 on Earth's surface, the equation can be rearranged to solve for time:
on Earth's surface, the equation can be rearranged to solve for time:
![\[ \text{Distance fallen} = (1)/(2) * g * \text{time}^2 \]](https://img.qammunity.org/2020/formulas/physics/middle-school/y9fin1sa0ag6c24bu24p5offignkjf9r36.png)
![\[ \text{time} = \sqrt{\frac{2 * \text{Distance fallen}}{g}} \]](https://img.qammunity.org/2020/formulas/physics/middle-school/25a2ineem61w3np86bw72h2cjnabs97icd.png)
Substituting the known values:
![\[ \text{time} = \sqrt{\frac{2 * 4.0 \, \text{m}}{9.81 \, \text{m/s}^2}} \]](https://img.qammunity.org/2020/formulas/physics/middle-school/ud5dwl30rmpzdwdmj2u25jzxvzptxrju1s.png)
![\[ \text{time} \approx √(0.814) \, \text{s} \]](https://img.qammunity.org/2020/formulas/physics/middle-school/o2lizv9l7ocw0p18j38r9ywrjv7fxfew3f.png)
![\[ \text{time} \approx 0.902 \, \text{s} \]](https://img.qammunity.org/2020/formulas/physics/middle-school/1c67il1n0wfy6dnkh736g00gw1xin3yeis.png)
Therefore, the acorn falls for approximately 0.902 seconds before landing on the dog's head.
Question
A squirrel drops an acorn onto the head of an unsuspecting dog. The acorn falls 4.0m before it lands on the dog. We can ignore air resistance. How many seconds did the acorn fall?