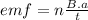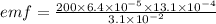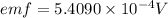Answer:
A)
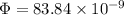
B)
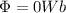
C)
Step-by-step explanation:
Given that:
- no. of turns i the coil,
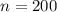
- area of the coil,

- time interval of rotation,
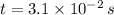
- intensity of magnetic field,
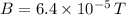
(A)
Initially the coil area is perpendicular to the magnetic field.
So, magnetic flux is given as:
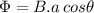 ..................................(1)
..................................(1)
 is the angle between the area vector and the magnetic field lines. Area vector is always perpendicular to the area given. In this case area vector is parallel to the magnetic field.
is the angle between the area vector and the magnetic field lines. Area vector is always perpendicular to the area given. In this case area vector is parallel to the magnetic field.
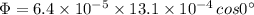

(B)
In this case the plane area is parallel to the magnetic field i.e. the area vector is perpendicular to the magnetic field.
∴
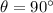
From eq. (1)
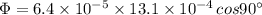
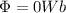
(C)
According to the Faraday's Law we have: