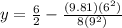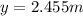Question

Two stones are thrown simultaneously, one straight upward from the base of a cliff and the other straight downward from the top of the cliff. The stones are thrown with the same speed.(a) Does the stone thrown upward gain or lose speed as it moves upward? Why?(b) Does the stone thrown downward gain or lose speed as time passes? Explain.(c) The speed at which the stones are thrown is such that they cross paths. Where do they cross paths, above, at, or below the point that corresponds to half the height of the cliff? Justify your answer. The height of the cliff is 6.00 m, and the speed with which the stones are thrown is 9.00 m/s. Find the location of the crossing point.

Answer 1

Part a)

The stone which is thrown upwards will lose its speed as it is moving opposite to gravity

Part b)

The speed of stone which is thrown downwards will increase with time as it moves under gravity.

Part c)

`y = (d)/(2) - (gd^2)/(8v^2)`

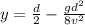
so it is less than the half of the total height

`y = 2.455 m`

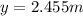
Step-by-step explanation:

Part a)

The stone which is thrown upwards will lose its speed as it is moving opposite to gravity

So due to gravitational force the speed of that stone will decrease with time

Part b)

The speed of stone which is thrown downwards will increase with time as it moves under gravity.

The gravitational force on that stone will increase the speed of the stone.

Part c)

the relative speed of two stone is given as

`v_r = 2v`

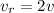
so the time at which two stone will cross the path is given as

`t = (d)/(2v)`

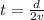
now the position at which the two stone cross the path is given as

`y = vt - (1)/(2)gt^2`

`y = (d)/(2v)(v) - (1)/(2)g((d)/(2v))^2`

`y = (d)/(2) - (gd^2)/(8v^2)`

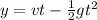
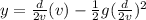
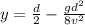
so it is less than the half of the total height

now plug in the given values

v = 9 m/s

d = 6 m

`y = (6)/(2) - ((9.81)(6^2))/(8(9^2))`

`y = 2.455 m`