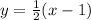Question

Identify an equation in point-slope form for the line parallel to y = 1/2 x-7 that

passes through (-3,-2).​

Answer 1

m= 1/2

Explanation:

i think you could take 1/2 and multiply it by -3,-2 and get yor answer or you could use 1/2

Answer 2

The equation of the line that is parallel to the line
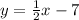`y=(1)/(2) x-7` and passes through the point (-3, -2) is
`\bold{y=(1)/(2)(x-1)}`

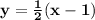
Solution:

Given that the line passes through point (-3, -2)

The line is parallel to
`y=(1)/(2) x-7 \rightarrow (1)`

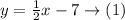
First let us find the slope of line, the point slope form is given as,

`y-y_(1)=m\left(x-x_(1)\right) \rightarrow (2)`

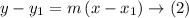
where "m" is the slope of line

Comparing the (1) with (2) we get, m=\frac{1}{2}

The slopes of parallel lines are always equal. Hence the slope of line passing through (-3, -2) has the same slope as m=\frac{1}{2}

Now plug in m=\frac{1}{2} and in (2) to get the required equation of line,

`y-(-2)=(1)/(2)(x-(-3)) \rightarrow y-(-2)=(x)/(2)+(3)/(2) \rightarrow y=(x)/(2)+(3)/(2)-2`

`y=(x)/(2)+(3)/(2)-(4)/(2)`

`y=(x)/(2)-(1)/(2) \rightarrow y=(1)/(2)(x-1)`

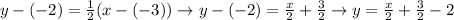
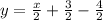
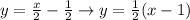
Thus, the equation of line parallel to given line is
`y=(1)/(2)(x-1)`