Question

Wind farm configuration is a significant issue as the upwind turbines generate maximal energy while creating wakes for downwind turbines. One measurement of interest is the wake expression parameter, WEP. A random sample of 180 WEP measurements in rescaled units has mean 26.7 and standard deviation 17.7. (a) Compute a 95% confidence interval for the true mean WEP. (b) Does the true mean WEP differ from 30? Explain.

Answer 1

a) [24.114,29.2858]

b) Since 30 is not in the 95% confidence interval, there is a 95% probability that 30 is not the true mean WEP

Explanation:

a)

The 95% confidence interval is given by the interval

`\bf [ \bar x-z^*(s)/(\sqrt n), \bar x+t^*(s)/(\sqrt n)]`

where

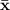`\bf \bar x`= 26.7 is the sample mean

s = 17.7 is the sample standard deviation

n = 180 is the sample size

Since the sample size is big enough, we can use the Normal N(0,1) to compute
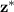`\bf z^*` and it would be 1.96(*) (a value such that the area under the Normal curve outside the interval [-z, z] is 5% (0.05))

and our 95% confidence interval is

`\bf [26.7-1.96*(17.7)/(√(180)), 26.7+1.96*(17.7)/(√(180))]=\boxed{[24.114,29.2858]}`

(*)

This value can be computed in Excel with

NORMINV(1-0.025,0,1)

and in OpenOffice Calc with

NORMINV(1-0.025;0;1)

b)

Since 30 is not in the 95% confidence interval, there is a 95% probability that 30 is not the true mean WEP