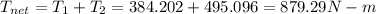Question

Two children hang by their hands from the same tree branch. The branch is straight, and grows out from the tree trunk at an angle of 27.0° above the horizontal. One child, with a mass of 44.0 kg, is hanging 1.00 m along the branch from the tree trunk. The other child, with a mass of 27.0 kg, is hanging 2.10 m from the tree trunk. What is the magnitude of the net torque exerted on the branch by the children? Assume that the axis is located where the branch joins the tree trunk and is perpendicular to the plane formed by the branch and the trunk.

Answer 1

Answer:879.29 N-m

Step-by-step explanation:

Given

mass of first child
`m_1=44 kg`

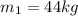
distance of first child from tree is
`r_1=1 m`

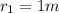
tree is inclined at an angle of
`\theta =27^(\circ)`

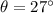
mass of second child
`m_1=27 kg`

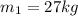
distance of second child from tree is
`r_2=2.1 m`

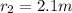
Weight of first child
`=m_1g=431.2 kg`

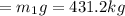
Weight of second child
`=m_2g=264.6 kg`

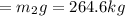
Torque of first child weight
`=m_1g\cos \theta \cdot r_1`

`T_1=44* 9.8* \cos 27* 1=384.202 N-m`

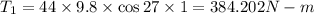
Torque of second child weight
`=m_2g\cos \theta \cdot r_2`

`T_2=27* 9.8* \cos 27* 2.1=495.096 N-m`

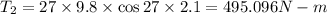
Net torque
`T_(net)=T_1+T_2=384.202+495.096=879.29 N-m`