Question

You measure the lifetime of a random sample of 64 tires of a certain brand. The sample mean is x¯=50 months. Suppose that the lifetimes for tires of this brand follow a Normal distribution, with unknown mean µ and standard deviation σ=5 months, then a 99% confidence interval for µ is:

Answer 1

(48.3875, 51.6125)

Explanation:

At 99% level of significance

`\alpha=1-0.99=0.01`

`Z_(a\lpha /2)=0.01/2=0.005`

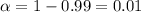
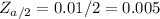
From the normal standard deviation table
`Z_(a\lpha /2)=2.33`

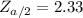
Considering that

`\bar x` ±
`Z_(a\lpha /2) \frac {\sigma}{√(n)}`=50±
`2.33\frac {5}{\sqrt {64}}`

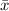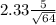
50±2.33(0.625)=50±1.6125=(48.3875, 51.6125)

Therefore, there’s 99% confidence that the mean lifetime of a certain brand of tires is between 48.3875 and 51.6125