Question

You are a member of an alpine rescue team and must get a box of supplies, with mass 2.20 kg , up an incline of constant slope angle 30.0 ∘ so that it reaches a stranded skier who is a vertical distance 3.10 m above the bottom of the incline. There is some friction present; the kinetic coefficient of friction is 6.00×10−2. Since you can't walk up the incline, you give the box a push that gives it an initial velocity; then the box slides up the incline, slowing down under the forces of friction and gravity. Take acceleration due to gravity to be 9.81 m/s2 .

Use the work-energy theorem to calculate the minimum speed v that you must give the box at the bottom of the incline so that it will reach the skier.

Answer 1

The minimum speed of the box bottom of the incline so that it will reach the skier is 8.19 m/s.

Step-by-step explanation:

It is given that,

Mass of the box, m = 2.2 kg

The box is inclined at an angle of 30 degrees

Vertical distance, d = 3.1 m

The coefficient of friction,
`\mu=6* 10^(-2)`

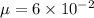
Using the work energy theorem, the loss of kinetic energy is equal to the sum of gain in potential energy and the work done against friction.

`KE=PE+W`

`(1)/(2)mv^2=mgh+W`

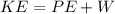
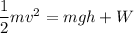
W is the work done by the friction.

`W=f* d`

`f=\mu mg\ cos\theta`

`W=\mu mg\ cos\theta* (d)/(sin\theta)`

`W=(\mu mgh)/(tan\theta)`

`(1)/(2)mv^2=mgh+(\mu mgh)/(tan\theta)`

`(1)/(2)v^2=gh+(\mu gh)/(tan\theta)`

`(1)/(2)v^2=9.8* 3.1+(6* 10^(-2)* 9.8* 3.1)/(tan(30))`

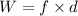
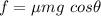
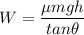
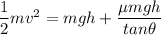
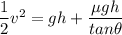
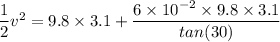
v = 8.19 m/s

So, the speed of the box is 8.19 m/s. Hence, this is the required solution.