Question

Consider a binomial distribution of 200 trials with expected value 80 and standard deviation of about 20.3. Use the criterion that it is unusual to have data values more than 2.5 standard deviations above the mean or 2.5 standard deviations below the mean to answer the following questions.(a) Would it be unusual to have more than 120 successes out of 200 trials? Explain.1. Yes. 120 is more than 2.5 standard deviations above the expected value.2.Yes. 120 is more than 2.5 standard deviations below the expected value. 3. No. 120 is less than 2.5 standard deviations above the expected value.4.No. 120 is less than 2.5 standard deviations below the expected value.(b) Would it be unusual to have fewer than 40 successes out of 200 trials? Explain.1.Yes. 40 is more than 2.5 standard deviations above the expected value.2.Yes. 40 is more than 2.5 standard deviations below the expected value. 3.No. 40 is less than 2.5 standard deviations above the expected value.4.No. 40 is less than 2.5 standard deviations below the expected value.(c) Would it be unusual to have from 70 to 90 successes out of 200 trials? Explain.1.Yes. 70 to 90 observations is within 2.5 standard deviations of the expected value.2.No. 70 to 90 observations is within 2.5 standard deviations of the expected value. 3. Yes. 70 observations is more than 2.5 standard deviations below the expected value.4.No. 90 observations is more than 2.5 standard deviations above the expected value.Expert Answer

Answer 1

See explanation below

Explanation:

In a binomial distribution of n trials the expected value is

E = np

where p is the probability of “success” and the standard deviation is

`\bf s=√(np(1-p))`

So, if the expected value is 80, then

80 = 200p

hence

p=2/5

The standard deviation would be

`\bf s=√(200*(2/5)*(3/5))=6.9282`

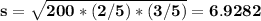
as a consequence it is not possible for a binomial distribution of 200 trials with expected value 80 to have a standard deviation of 20.3