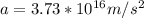Question

An electron moves at 2.80 ×106 m/s through a region in which there is a magnetic field of unspecified direction and magnitude 7.60 ×10−2 T. Part A What is the largest possible magnitude of the acceleration of the electron due to the magnetic field? Express your answer with the appropriate units. aa = nothing

Answer 1

`a = 3.73*10^(16)m/s^2`

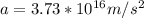
Step-by-step explanation:

The magnetic force is given by the equation,

`\vec{F}_(magnetic) = q (\vec{v}X\vec{B})`

`\vec{F}_(magnetic) = qvBsin\theta`

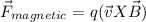
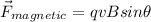
Where
`\theta` is the angle between velocity vector and the magnetic field,

That angle is 90°.

We know as well that

F=ma, replacing the mass and the acceleration in our previous equation we have

`ma = qvBsin\theta`

`a= (qvBsin\theta)/(m)`

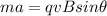
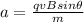
Our values are,

`q= 1.6*10^(-19)c`

`v=2.8*10^6m/s`

`B=7.6*10^(-2)T`

`m=9.11*10^(-31)kg`

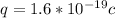
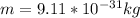
Substituting,

`a = ((1.6*10^(-19))(2.8*10^6)(7.6*10^(-2)))/(9.11*10^(-31))`

`a = 3.73*10^(16)m/s^2`