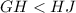Answer:
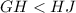
Explanation:
We are given that
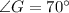
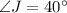
We have to fill the correct symbol in the blank space.
Greater angle and greater side theorem: It states that when
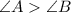
Then, Opposite side to angle A > opposite side to angle B.
When Opposite side to angle A > opposite side to angle B
Then,
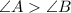
Side opposite to angle J=GH
Side opposite to angle G=HJ
Using the above theorem,
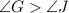
Then,
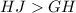
Hence,