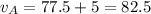We can model the problem as follows: on a number line we put train A, with positive speed
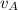 , at the origin x=0.
, at the origin x=0.
At x=480 we put train B, with negative speed
 .
.
So, the equations for the positions of the two trains are
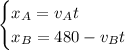
We know that
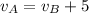 , so we can rewrite the first equation:
, so we can rewrite the first equation:
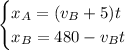
The two trains meet when they are at the same position:
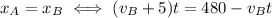
We know that this happens after 3 hours, i.e. when t=3:
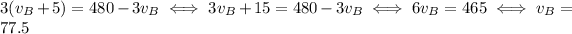
And since train A was 5 mph faster, we have