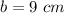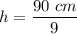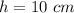Question

PLEASE HELP!! Determine the height of a triangle with an area of 45 cm2 and a base that is 9 cm long.

Answer 1

`h = (2A)/(b)`

`h = 10~cm`

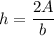
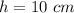
Explanation:

Do the first part of the problem first. Solve the area formula for the height.

Start with the area formula:

`A = (1)/(2)bh`

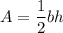
Switch sides.

`(1)/(2)bh = A`

Multiply both sides by 2.

`2 * (1)/(2)bh = 2 * A`

`bh = 2A`

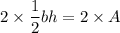
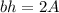
Divide both sides by b.

`h = (2A)/(b)`

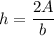
Now that you have the formula solved for h, plug in the numbers you are given for the area and the base, and evaluate the right side to find the height.

`h = (2A)/(b)`

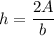
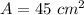`A = 45~cm^2` and
`b = 9~cm`

`h = (2 * 45~cm^2)/(9~cm)`

`h = (90~cm)/(9)`

`h = 10~cm`

Answer 2

Replace A and b in the given formula and solve for h:

45 = 1/2 x 9 x H

Simplify:

45 = 4.5 x H

Divide both sides by 4.5

H = 45 / 4.5

H = 10 cm

The height is 10 cm.