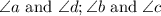Question

Two similar triangles are shown below:

Two triangles are shown. The sides of the triangle on the left are marked 6, 8, 4. The sides of the triangle on the right are marked as 3, 4, and 2. For the triangle on the left, the angle between sides marked 8 and 6 is labeled as a, marked by a double arc, and the angle between the sides marked 8 and 4 is labeled as b, marked by a single arc. The third angle is marked by a triple arc. For the triangle on the right, the angle between sides marked 2 and 4 is labeled as c, marked by a single arc and the angle between the sides marked 4 and 3 is labeled as d, marked by a double arc. The angle between the sides 2 and 3 is labeled as e, marked by a triple arc, and it is also the angle on the top vertex of this triangle.

Which two sets of angles are corresponding angles?

∠a and ∠d; ∠b and ∠c
∠a and ∠e; ∠b and ∠d
∠a and ∠c; ∠b and ∠d
∠a and ∠e; ∠b and ∠c

Answer 1

The answer is a and d + b and c

Explanation:

Answer 2

`\angle a \textrm{ and }\angle d; \angle b \textrm{ and }\angle c`

Explanation:

Given:

The triangles are drawn below.

The triangles ABC and DEF are similar.

So, corresponding sides are proportional.

Here,
`(AB)/(DE)=(6)/(3)=2`

`(BC)/(DF)=(8)/(4)=2`

`(AC)/(EF)=(4)/(2)=2`

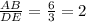
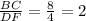
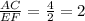
Therefore,
`(AB)/(DE)=(BC)/(DF)=(AC)/(EF)=2`

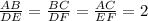
For similar triangles, the angles opposite corresponding sides are congruent and are called corresponding angles.

So, from the triangle, as sides AB and DE are corresponding sides, therefore, angles b and c are corresponding angles as they are opposite to sides AB and DE respectively.

Similarly, angles opposite to corresponding sides AC and EF are angles a and d respectively. So, angles a and d are corresponding angles.

Therefore, two sets of angles that are corresponding angles are:

`\angle a \textrm{ and }\angle d; \angle b \textrm{ and }\angle c`