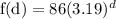Question

Initially, there were only 86 weeds in the garden. The weeds grew at a rate of 18% each week. The following function represents the weekly weed growth: f(x) = 86(1.18)x. Rewrite the function to show how quickly the weeds grow each day.

Answer 1

The function that shows how quickly the weeds grow each day is
`\text{f(d)} = 86(3.19)^{d`

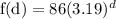
Rewriting the function to show how quickly the weeds grow each day.

From the question, we have the following parameters that can be used in our computation:

`\text{f(x)} = 86(1.18)^x`

Where

x is the number of weeks

There are 7 days in a week

So, we have

x = 7d

Where, d is the number of days

This means that

`\text{f(d)} = 86(1.18)^{7 * d`

Expand

`\text{f(d)} = 86(3.19)^{d`

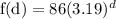
Hence, the function to show how quickly the weeds grow each day is
`\text{f(d)} = 86(3.19)^{d`

Answer 2

f(z) = 86.(0.169)z

Explanation:

Let's call

• x = number of weeks

• z = number of days

We have the growing function f(x) = 86.(1.18)x. If we want to write f in terms of z, we need to consider that x = z/7, since there are 7 days in each week. Then,

86.(1.18)x = 86.(1.18)z/7 = 86.(0.169)z

f(z) = 86.(0.169)z