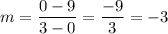Question

How do you find the average rate of change for f(x)=9-x^2 between two points: x=0 to x=3?

Please I have a final tomorrow and I’m clueless

Answer 1

The average rate of change is -3.

Explanation:

We are given the function:

`f(x)=9-x^2`

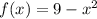
And we want to find the average rate of change from x = 0 to x = 3.

In other words, we will compute the function at the two endpoints, and then find the slope of the line that crosses the two points.

For our first endpoint at x = 0, our function evaluates to:

`f(0)=9-(0)^2=9`

So, our first point is (0, 9).

For our second endpoint at x = 3, our function evaluates to :

`f(x)=9-(3)^2=0`

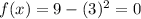
So, our second point is (3, 0).

Then by the slope formula, our average rate of change will be:

`\displaystyle m=(0-9)/(3-0)=(-9)/(3)=-3`