Question

NEED ANSWERS AND EXPLANATION ASAP!!!

1. Evaluate S₅ for 2500+2000+1600+1280+..


2. Evaluate S₁₄ for 11+3+(-5)+(-13)+...

Answer 1

see explanation

Explanation:

(1)

Note the ratio of consecutive terms is common, that is

2000 ÷ 2500 = 0.8

1600 ÷ 2000 = 0.8

1280 ÷ 1600 = 0.8

This indicates that the series is geometric with common ratio r = 0.8

The sum to n terms of a geometric series is

`S_(n)` =
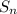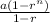`(a(1-r^n))/(1-r)` ← a is the first term

Here a = 2500 and r = 0.8, thus

`S_(5)` =
`(2500(1-0.8^5))/(1-0.8)` =
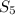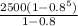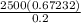`(2500(0.67232))/(0.2)` = 8404

(2)

Note the difference in consecutive terms is common, that is

3 - 11 = - 8

- 5 - 3 = - 8

- 13 - (- 5) = - 8

This indicates that the series is arithmetic with common difference d = - 8

The sum to n terms of an arithmetic series is

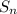`S_(n)` = a₁ + (n - 1)d ← a₁ is the first term

Here a₁ = 11 and d = - 8, thus

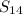`S_(14)` = 11 + (13 × - 8) = 11 - 104 = - 93