Question

Select all of the following statements that are true

All real numbers are natural numbers
All whole numbers are integers
All integers are whole numbers
All natural numbers are rational numbers
All irrational numbers are dense

Answer 1

2, 4, and 5

Explanation:

Just had the question asked on ed2020. :)

Answer 2

All whole numbers are integers.

All natural numbers are rational numbers.

All irrational numbers are dense.

Explanation:

1) All real numbers are natural numbers. - WRONG.

Consider
`$ √(2) $`. This is a real number but a natural number which consists of integers
`$ \{1 , 2 , 3 ,. . . \} $`.

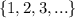2) All whole numbers are integers. - CORRECT.

Whole numbers consist of natural numbers and zero. i.e.,
`$ \{0, 1 , 2, . . . \}`. All these numbers are integers. Hence the statement is correct.

3) All integers are whole numbers. - WRONG.

Consider
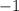`$ -1 $`. This is an integer. But not a whole number.

4) All natural numbers are rational numbers - CORRECT.

All natural numbers are a subset of rational numbers.i.e., rational numbers with denominator
`$ 1 $` , In fact they are a subset of real numbers as well. Hence the statement is correct.

Note that the converse isn't true,

5) All irrational numbers are dense - CORRECT.

All irrational and rational numbers are dense on a real line. This basically means that for any two irrational numbers on a real line there is always another irrational number between them. This holds for true for rational numbers as well.