Question

Restaurant A uses 60 bags of tomatoes each month. The tomatoes are purchased from a supplier for a price of $80 per bag and an ordering cost of $20 per order. Restaurant A’s annual inventory holding cost percentage is 40%. If Restaurant A chooses to use the economic order quantity when placing an order for tomatoes, what are its ordering and holding costs per year expressed as a percentage of the annual purchasing cost? A. 2% B. 3% C. 4% D. 5%

Answer 1

A. 2%

Step-by-step explanation:

The computation of the economic order quantity is shown below:

=
`\sqrt{\frac{2* \text{Annual demand}* \text{Ordering cost}}{\text{Carrying cost}}}`

where,

Annual demand = 60 bags × 12 months = 720 bags

Ordering cost = $20

Carrying or holding cost = Price × annual inventory holding cost percentage

= $80 × 40%

= $32

Now put these values to the above formula

So, the value would equal to

=
`\sqrt{\frac{2* \text{\$720}* \text{\$20}}{\text{\$32}}}`

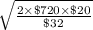
= 30 bags

The number of orders would be equal to

= Annual demand ÷ economic order quantity

= 720 ÷ 30

= 24 orders

c. The average inventory would equal to

= Economic order quantity ÷ 2

= 30 bags ÷ 2

= 15 bags

d. The total cost of ordering cost and carrying cost equals to

Ordering cost = Number of orders × ordering cost per order

= 24 orders × $20

= $480

Carrying cost = Average inventory × carrying cost per unit

= 15 bags × $32

= $480

So, the total would be

= $480 + $480

= $960

And, the total purchase cost = Annual demand × price per bag

= 720 × $80

= $57,600

Now the percentage would be

= Total cost ÷ Total purchase cost

= $960 ÷ $57,600

= 1.67%