Question

Write the quadratic equation whose roots are -3 and -6, and whose leading coefficient is 3

Answer 1

`$ 3x^2 + 27x + 54 = 0 $`

Explanation:

A quadratic equation is given by:
`$ a_1 x^2 + ax + b = 0 $`

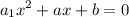
The leading co-efficient is
`$ a_1 $`.

Given
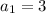`$ a_1 = 3$`. Therefore the quadratic equation becomes:

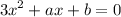`$ 3x^2 + ax + b = 0 $`. We are to find
`$ (a,b) $`.

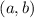Given the solutions of this equation are:
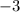`$ -3 $` and
`$ -6 $`.

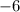Substituting this in the equation we get:

`$ 3(-3)^2 +a(-3) + b = 27 -3a + b = 0 \hspace{15mm} (1) $`

`$ 3(-6)^2 +a(-6) + b = 108 -6a + b = 0  \hspace{15mm} (2) $`

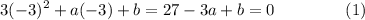
Solving
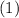`$ (1) $` and
`$ (2) $` we get

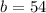`$ b = 54 $`. Substituting in
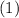`$ (1) $` we get

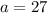`$ a = 27 $`. Thus the equation becomes:

`$ 3x^2 + 27x + 54 = 0 $`