Question

Your artist friend is designing an exhibit inspired by circular-aperture diffraction. A pinhole in a red zone is going to be illuminated with a red laser beam of wavelength 670 nm, while a pinhole in a violet zone is going to be illuminated with a violet laser beam of wavelength 410 nm. She wants all the diffraction patterns seen on a distant screen to have the same size.

For this to work, what must be the ratio of the red pinhole's diameter to that of the violet pinhole?

Dred/Dviolet=?

Answer 1

The minimum angle, I, of a light beam diffraction pattern from a circular aperture distance, D, can be calculated using the Rayleigh' criterion given as:

`θ=(1.22λ)/(D)`

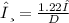
Step-by-step explanation:

Now the min angle of the red light zone diffraction pattern will be;

`θ1=(1.22x670x10^(-9))/(D1)`

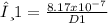`θ1=(8.17x10^(-7))/(D1)` . . . . . . . . . . . . . . . . . . . . Eqn 1

Similarly, the min angle of the violet light zone diffraction pattern will have;

`θ2=(1.22x410x10^(-9))/(D2)`

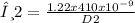
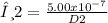`θ2=(5.00x10^(-7))/(D2)` . . . . . . . . . . . . . . . . . . . Eqn 2

However, remember that, we were told that the diffraction patterns seen on the distant screen have the same size. This means that the two diffractions have the same min angle, i

i.e, I1=I2=I

By this, we can then find the ratio of the pinhole diameters (D1 and D2) of each apertures.

Comparing Eqn 1 and 2 gives,

`(8.17x10^(-7))/(D1)=(5.00x10^(-7))/(D2)`

`(D1)/(D2)={1.633}`

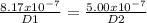
Hence, it means that the ratio of the red pinhole diameter D1, to that of the violet pinhole D2, must be 1.633 for the diffraction patterns to work.