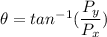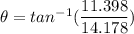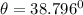Answer
given,
mass of truck = 2100 Kg
velocity in north direction = 41 km/h
= 41 x 0.278 m/s
= 11.398 m/s
velocity in north direction = 51 km/h
= 51 x 0.278 m/s
= 14.178 m/s
a) Change in K.E
=
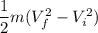
=
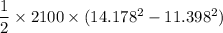
= 7.453 x 10⁴ J
b) Change in momentum
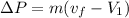
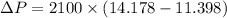
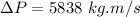
c) Direction of momentum