Answer:
Here, the wavelength of the light λ, that has a its 2nd order maximum m=2, at θ = 45.0º, when falling on a grating with 5000 lines per centimeter, can be calculated using the principle of diffraction grating which states that:
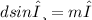 (See the attached illustration picture)
(See the attached illustration picture)
Step-by-step explanation:
Where;
d=distance between lines =
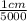 (Given in the question)
(Given in the question)
m = order of the maximum = 2
θ=angle of diffraction of the light = 45.0º
and
λ = wavelength of the light = Unknown?
Now, we can do the calculation as follows,
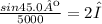
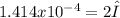
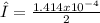
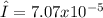
Hence, the wavelength of light that has its second-order maximum at 45.0º when falling on a diffraction grating that has 5000 lines per centimeter is 0.0000707cm