Question

In the economy of Ricardia, two consumer goods, X and Y, are produced from a single factor input, labor, according to the production functions: Y = 3Ly and X = 3Lx where Ly and Lx are the quantities of labor used in the production of Y and X respectively. The total amount of labor available is 66 units. (a) Derive the equation for the economy's production possibility frontier. Confirm that the marginal rate of transformation is equal to MPLy/MPLx.

Answer 1

`(a_y)/(a_x)`

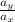
Step-by-step explanation:

Remember that the production possibilities frontier represents the amount of production that can be obtained from a certain number of factors. Therefore, goods (production) must be in function, since the factors are exogenous and given.

We have:

`Y\ =3L_y` and
`X\ =3L_x` are the units of labor dedicated to each good. And we know that:

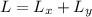`L=L_x + L_y` Total available labor is distributed between the two goods.

We can express the workforce of each good as the product of the production of the good by the work requirement per unit of product for each good, in this way:

`L_x =a_xX`,

`L_y =a_yY`,

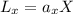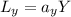Where
`a_x` and
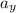`a_y` are the requirements.

If we isolate any good, in this case X, we have to:

`X=(L)/(a_x)-(a_y)/(a_x) \cdot Y`

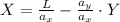
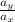`(a_y)/(a_x)` is the marginal rate of transformation or the rate at which the economy can transform X for Y.